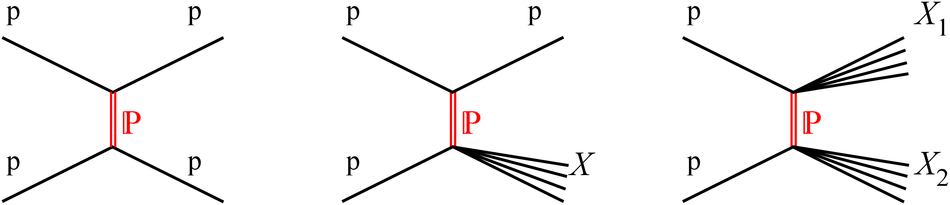
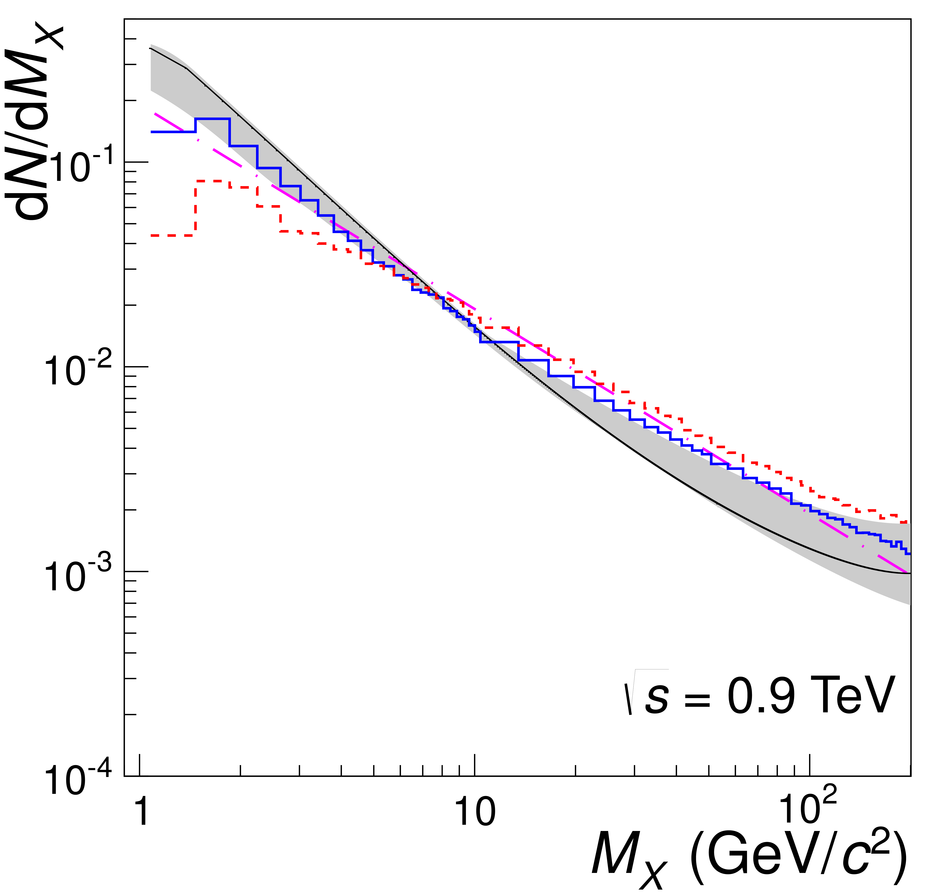
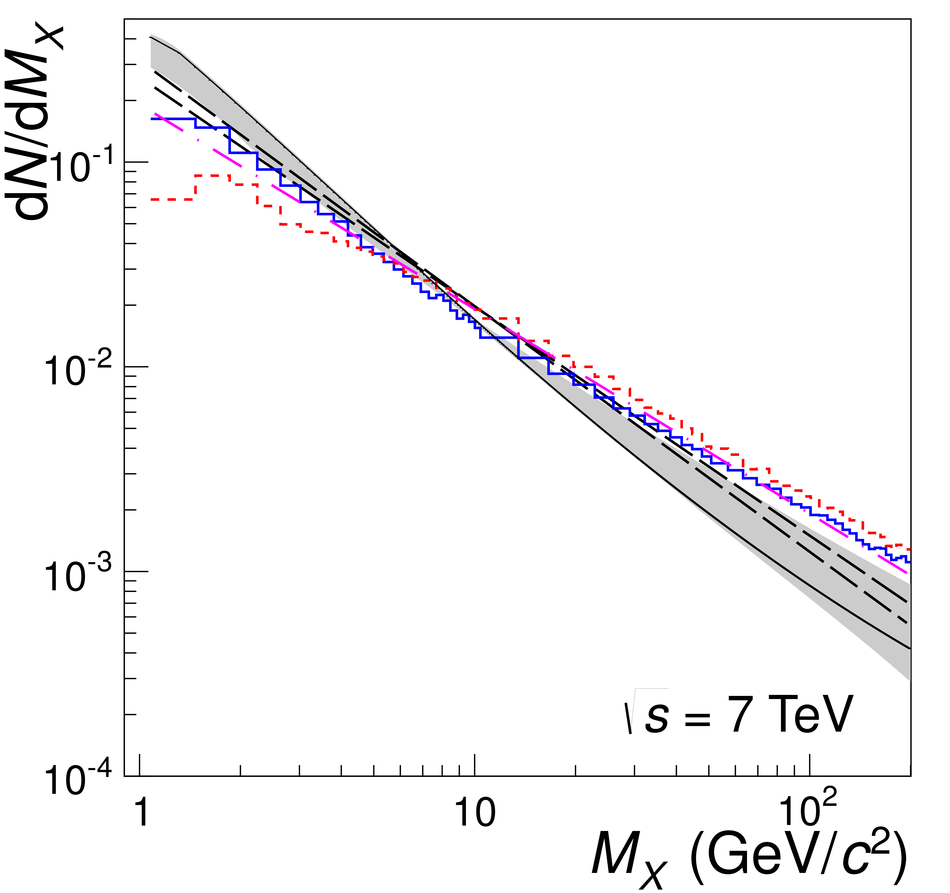
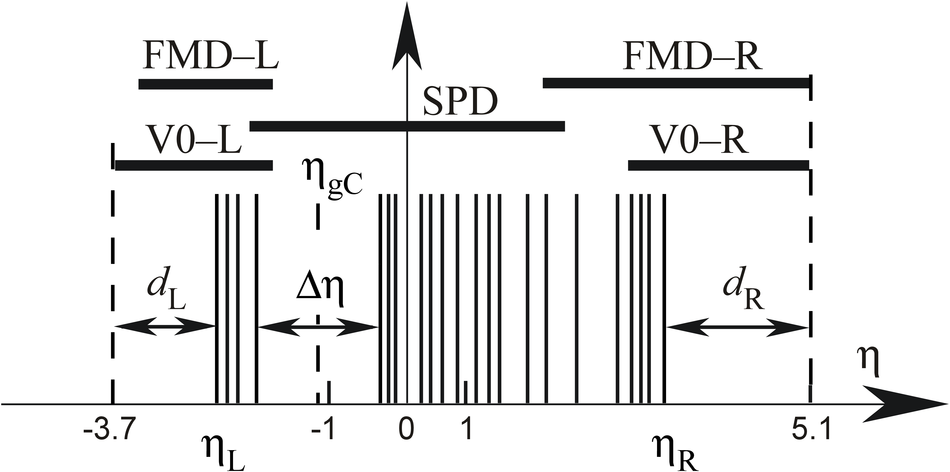
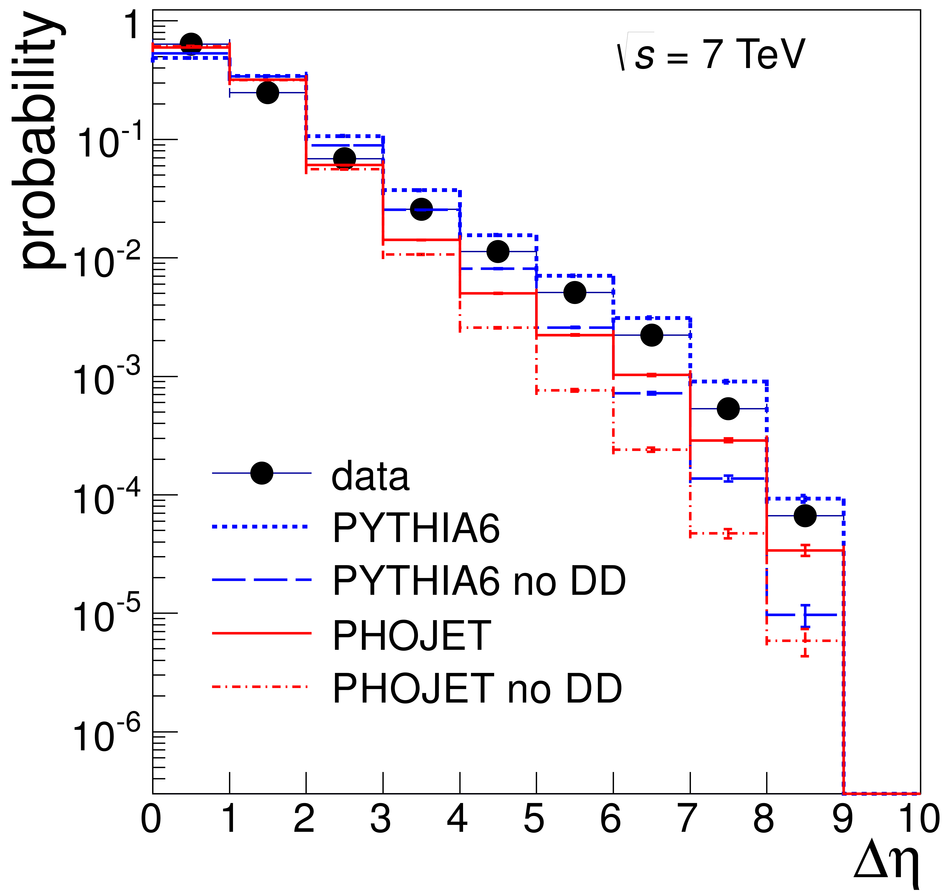
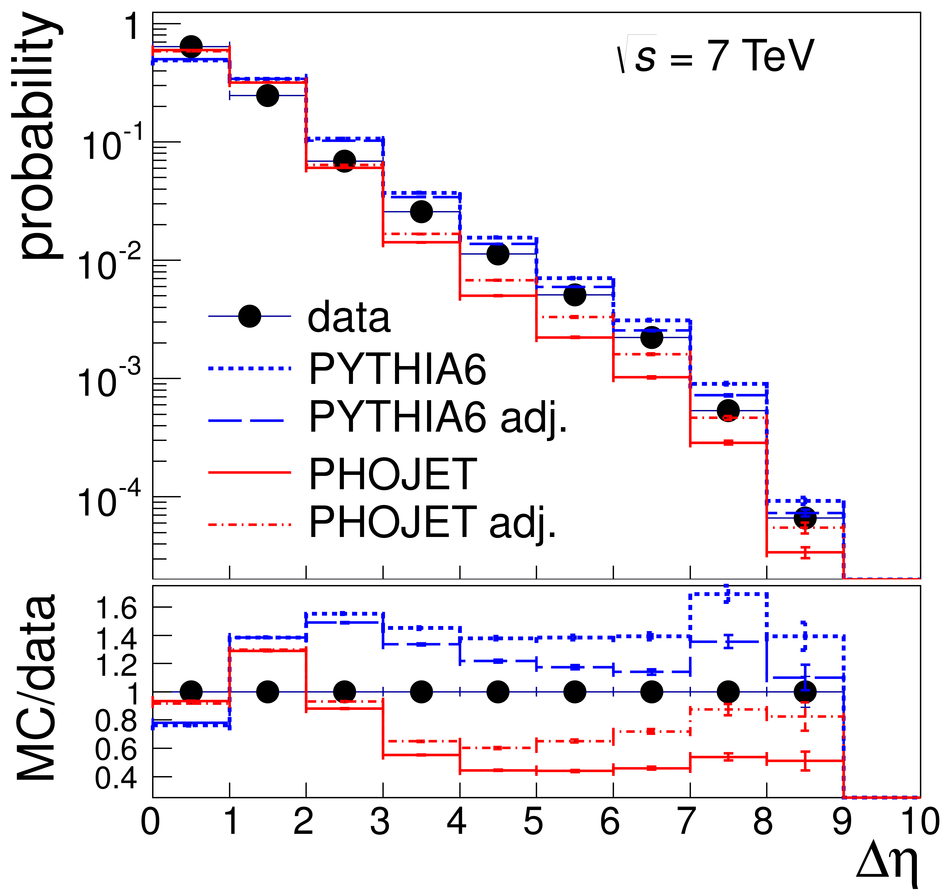
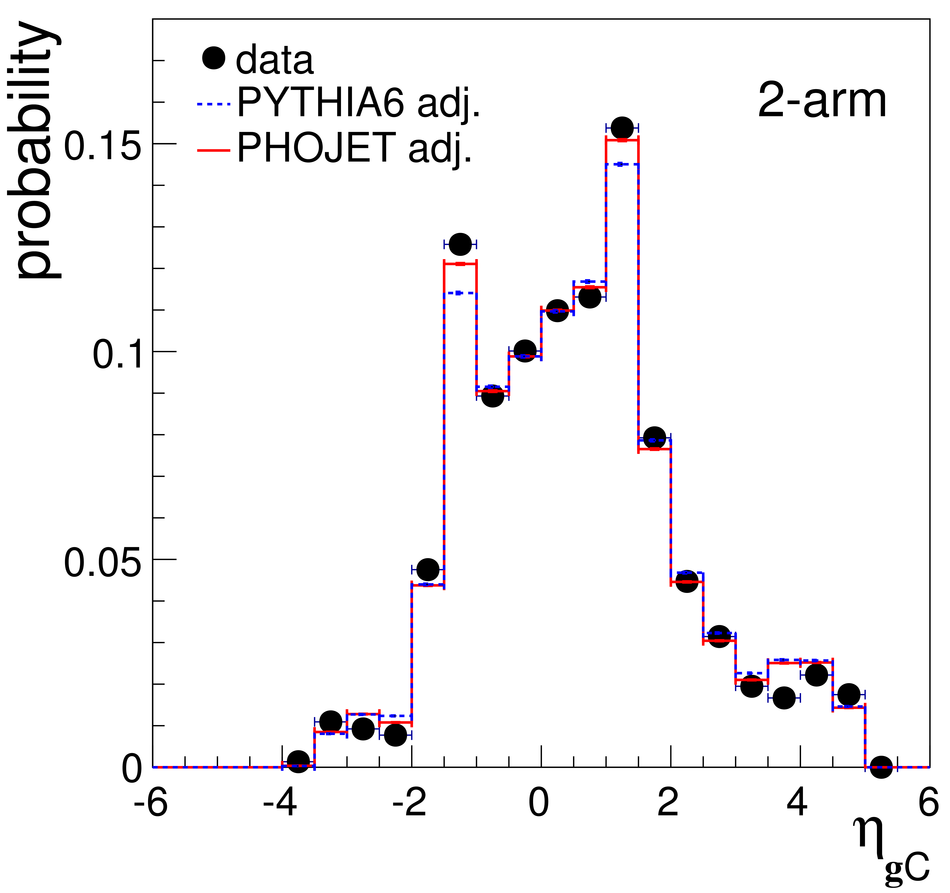
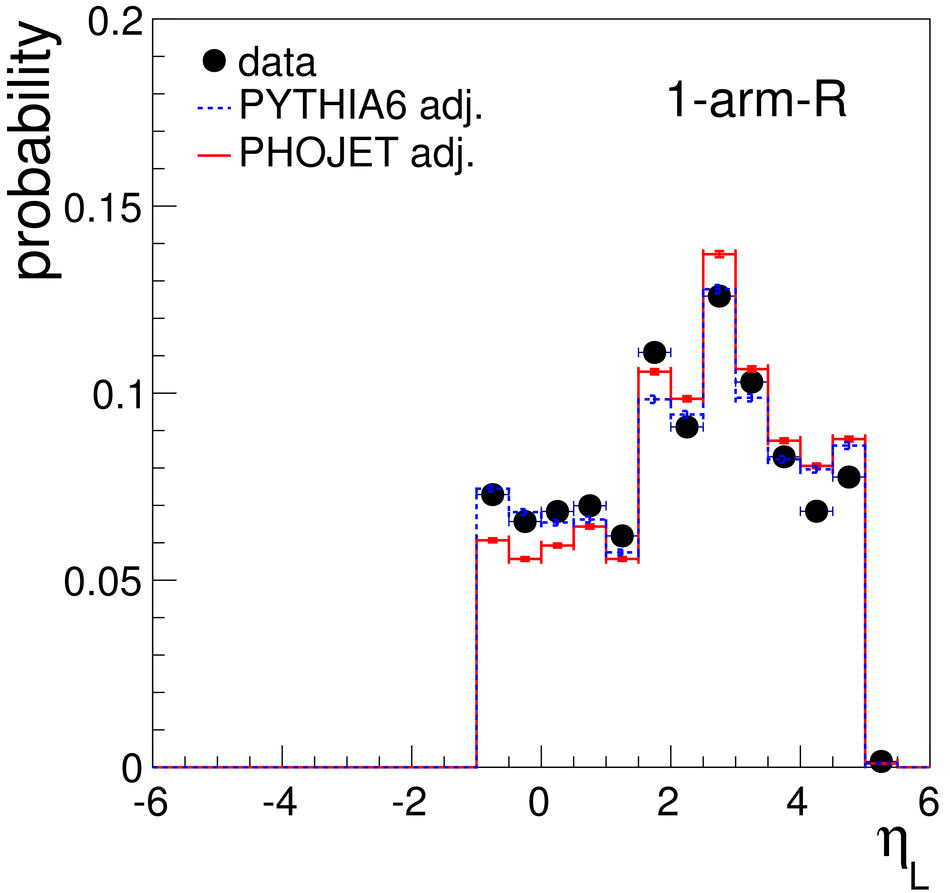
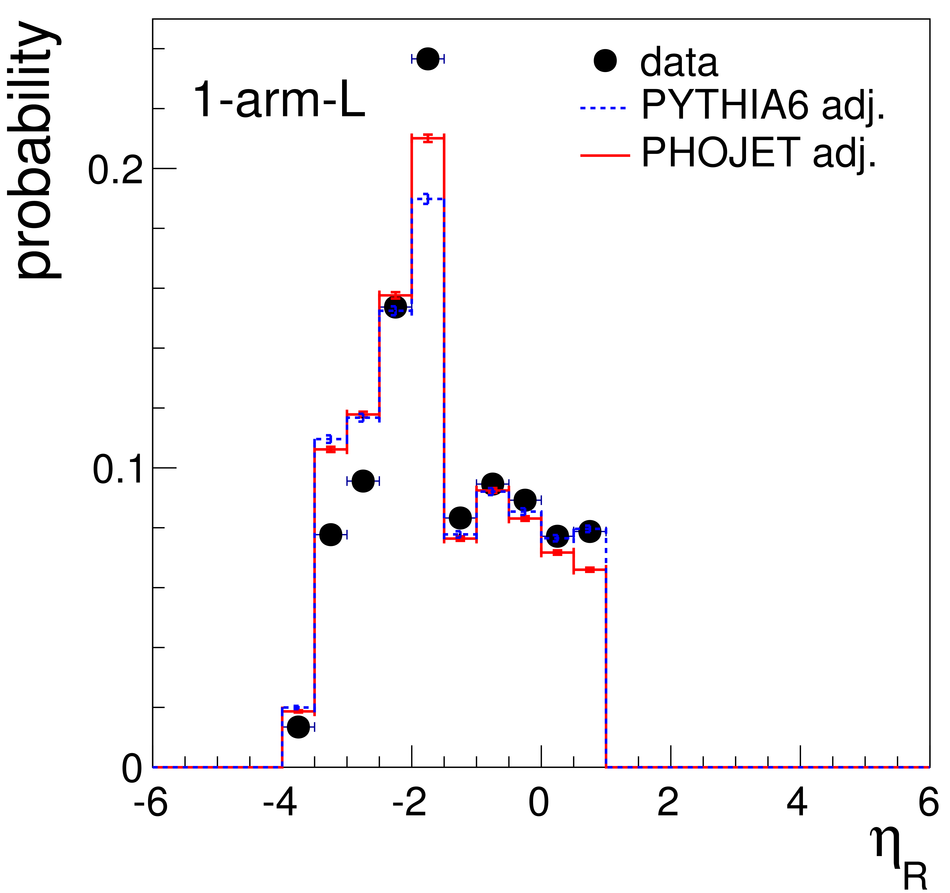
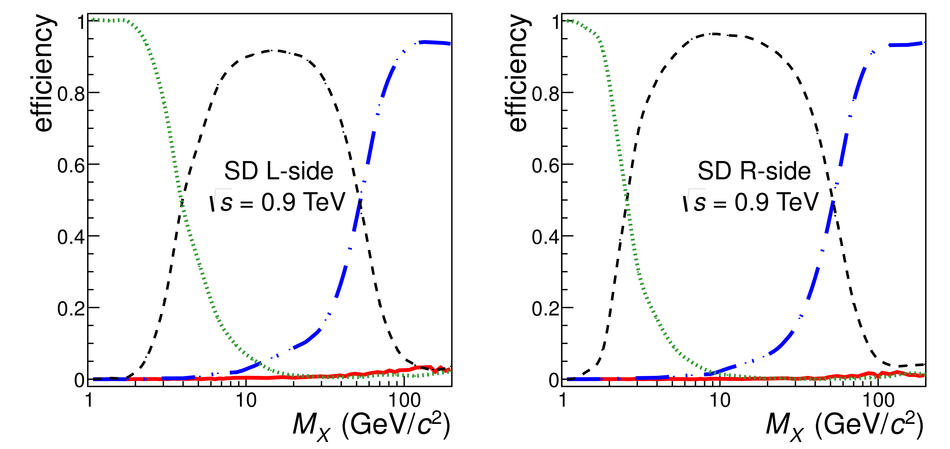
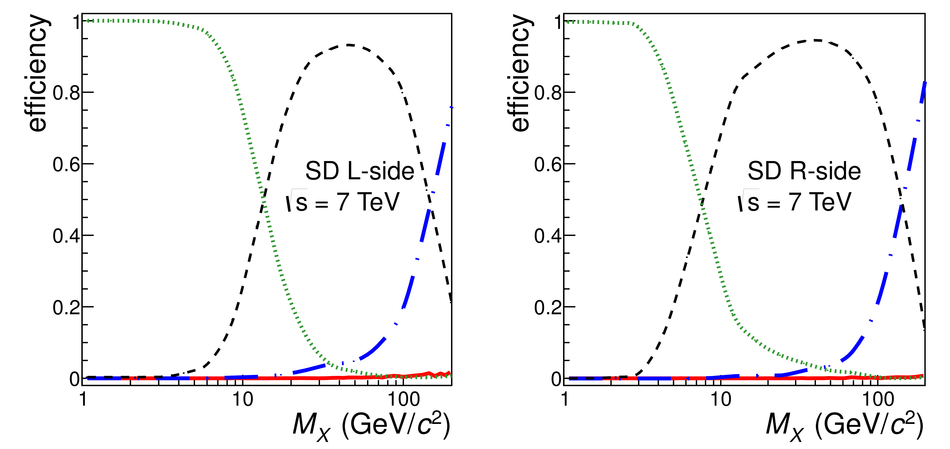
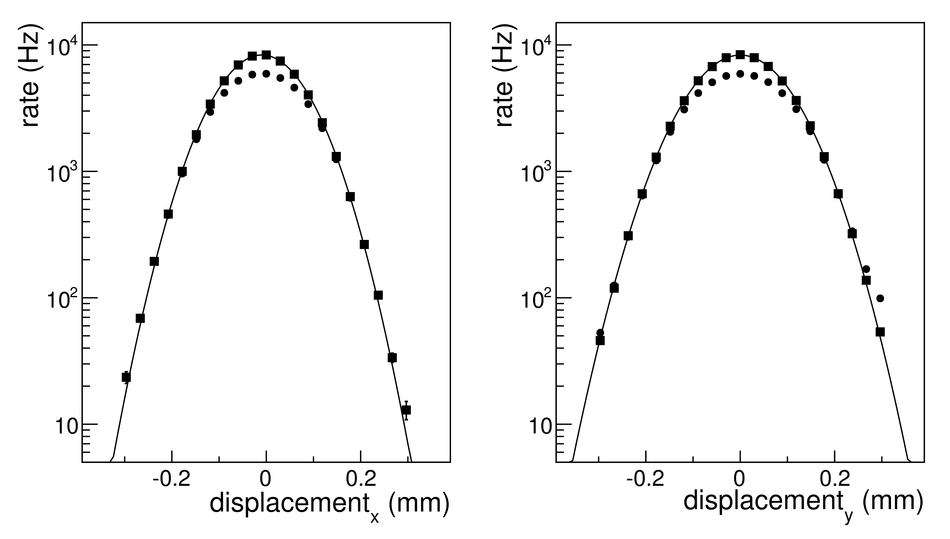
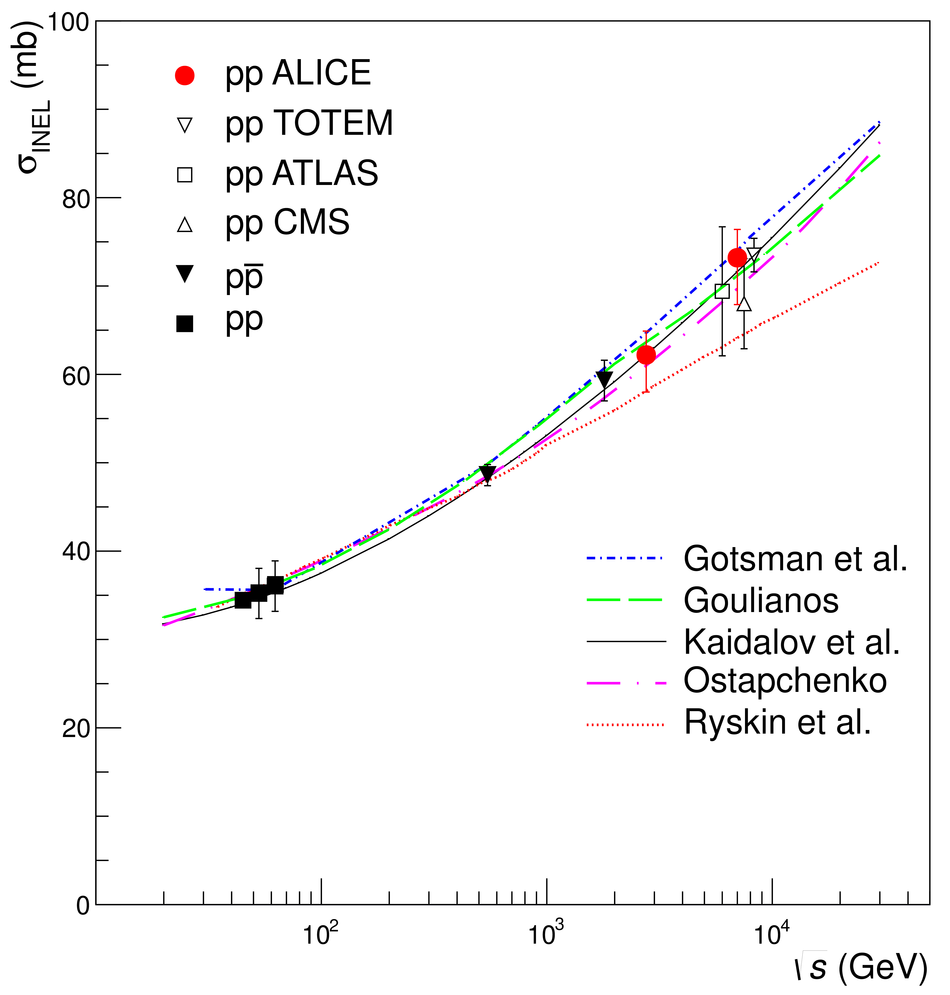
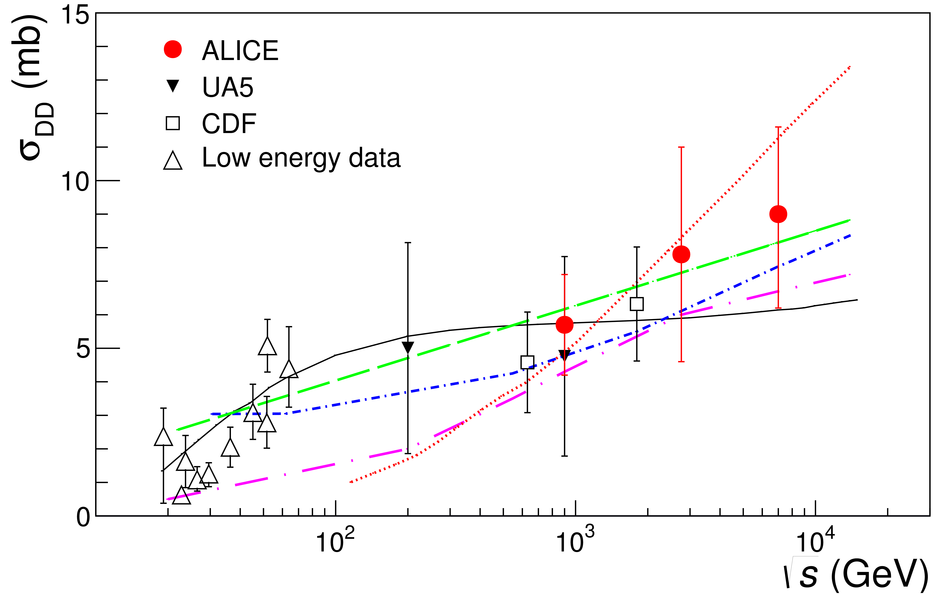
Measurements of cross sections of inelastic and diffractive processes in proton--proton collisions at LHC energies were carried out with the ALICE detector. The fractions of diffractive processes in inelastic collisions were determined from a study of gaps in charged particle pseudorapidity distributions: for single diffraction (diffractive mass $M_X <~ 200$ GeV/$c^2$) $\sigma_{\rm SD}/\sigma_{\rm INEL} = 0.21 \pm 0.03, 0.20^{+0.07}_{-0.08}$, and $0.20^{+0.04}_{-0.07}$, respectively at centre-of-mass energies $\sqrt{s} = 0.9, 2.76$, and 7~TeV; for double diffraction (for a pseudorapidity gap $\Delta\eta > 3$) $\sigma_{\rm DD}/\sigma_{\rm INEL} = 0.11 \pm 0.03, 0.12 \pm 0.05$, and $0.12^{+0.05}_{-0.04}$, respectively at $\sqrt{s} = 0.9, 2.76$, and 7~TeV. To measure the inelastic cross section, beam properties were determined with van der Meer scans, and, using a simulation of diffraction adjusted to data, the following values were obtained: $\sigma_{\rm INEL} = 62.8^{+2.4}_{-4.0} (model) \pm 1.2 (lumi)$ mb at $\sqrt{s} =$ 2.76~TeV and $73.2^{+2.0}_{-4.6} (model) \pm 2.6 (lumi)$ mb at $\sqrt{s}$ = 7~TeV. The single- and double-diffractive cross sections were calculated combining relative rates of diffraction with inelastic cross sections. The results are compared to previous measurements at proton--antiproton and proton--proton colliders at lower energies, to measurements by other experiments at the LHC, and to theoretical models.
Eur. Phys. J. C 73 (2013) 2456
e-Print: arXiv:arXiv:1208.4968 | PDF | inSPIRE
CERN-PH-EP-2012-238