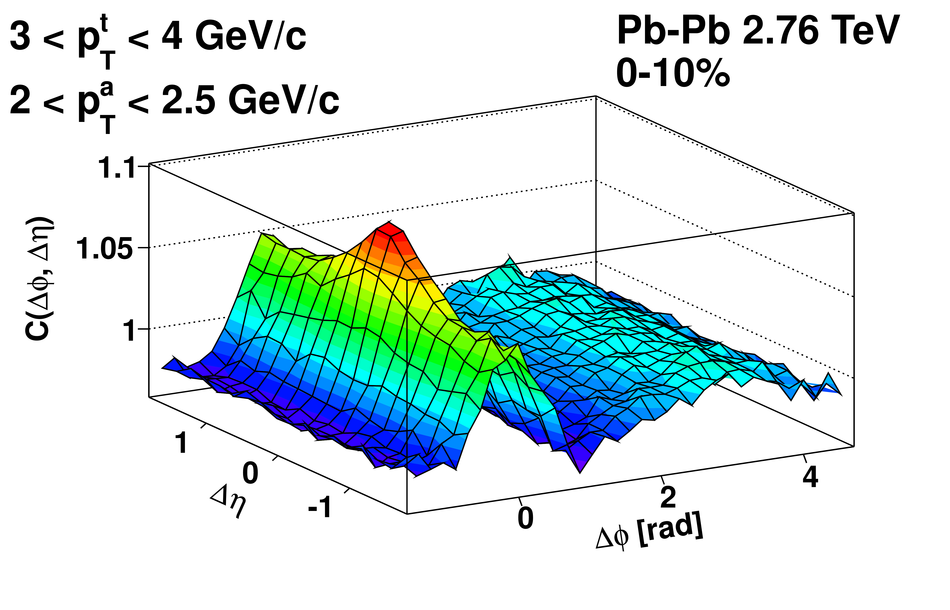
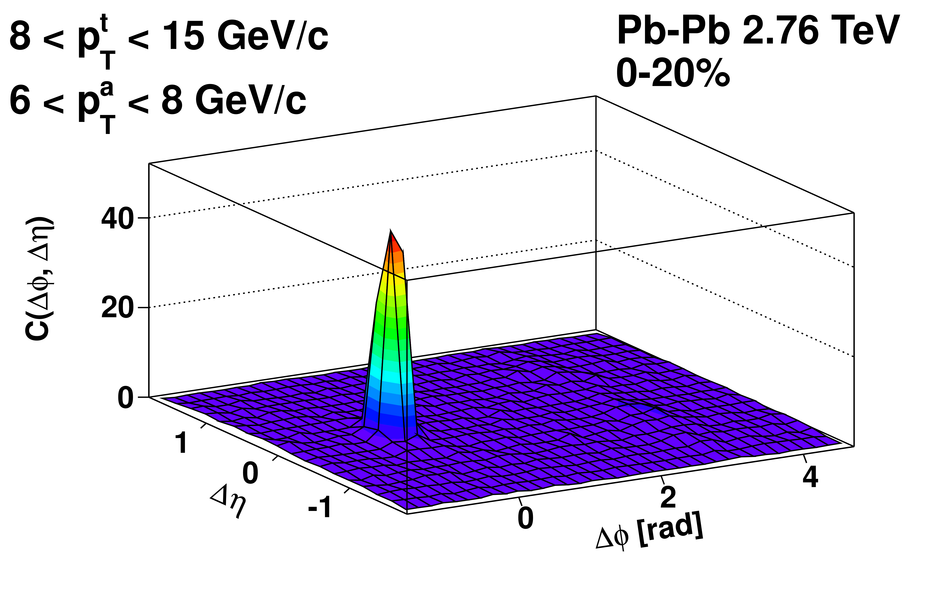
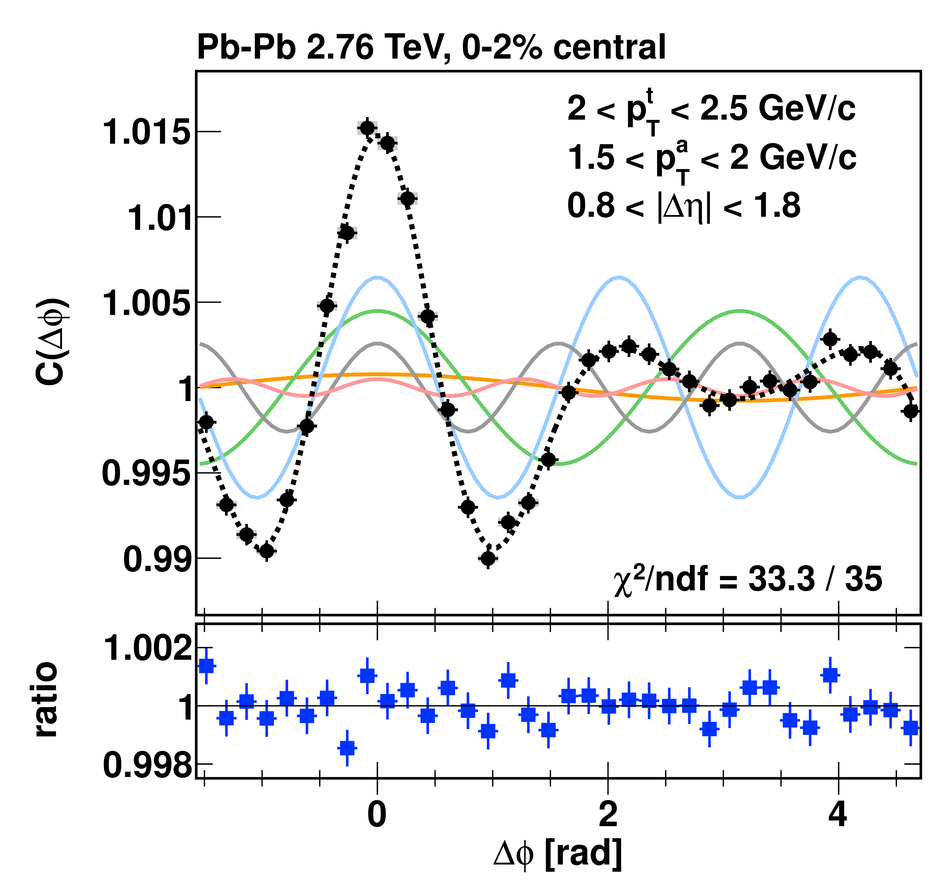
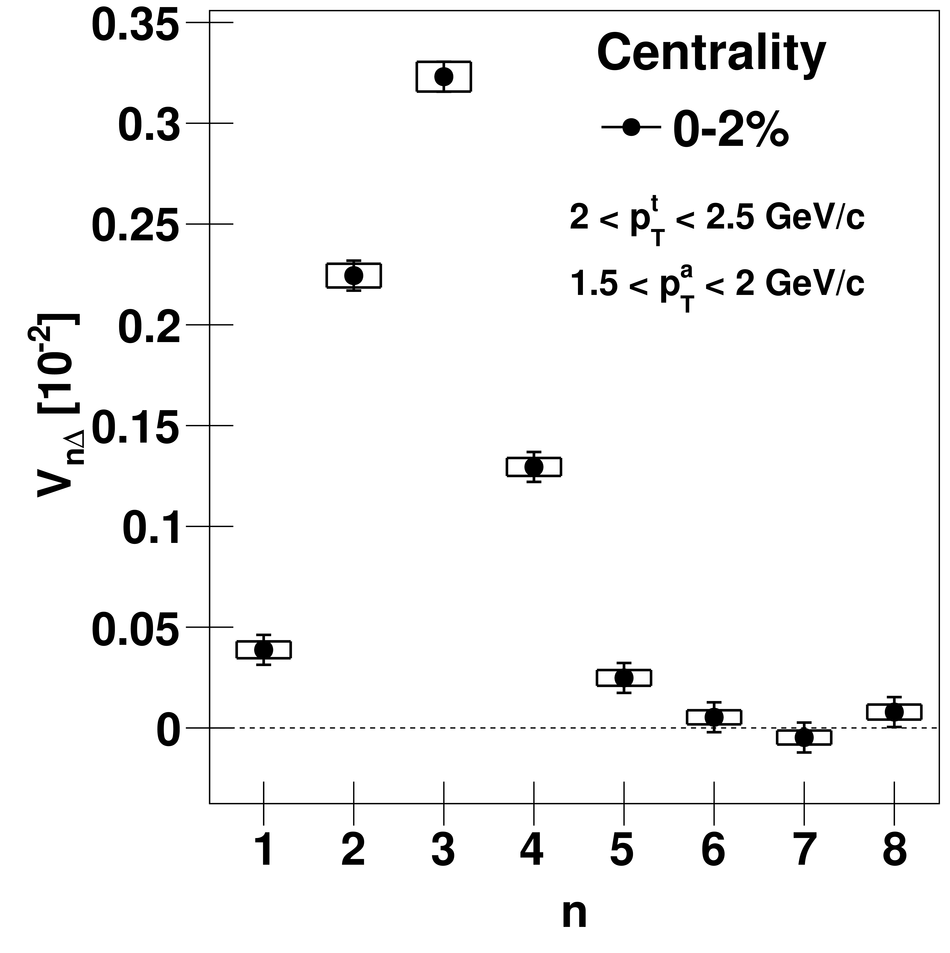
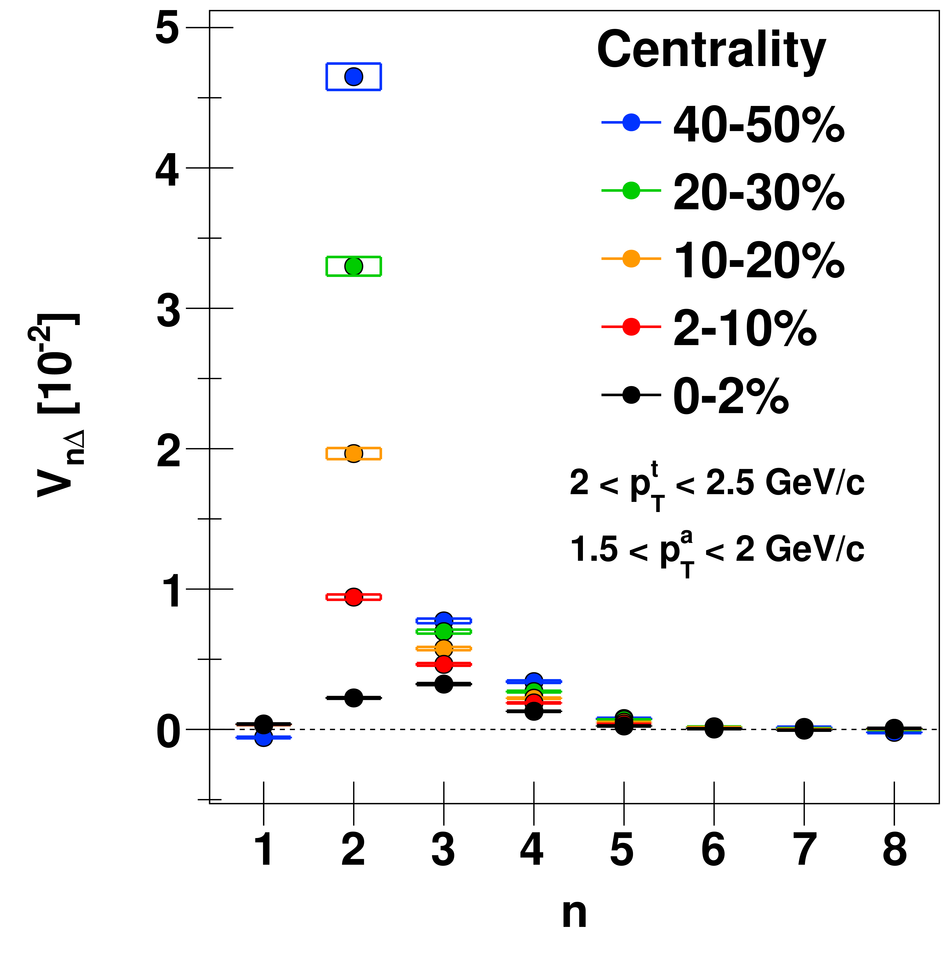
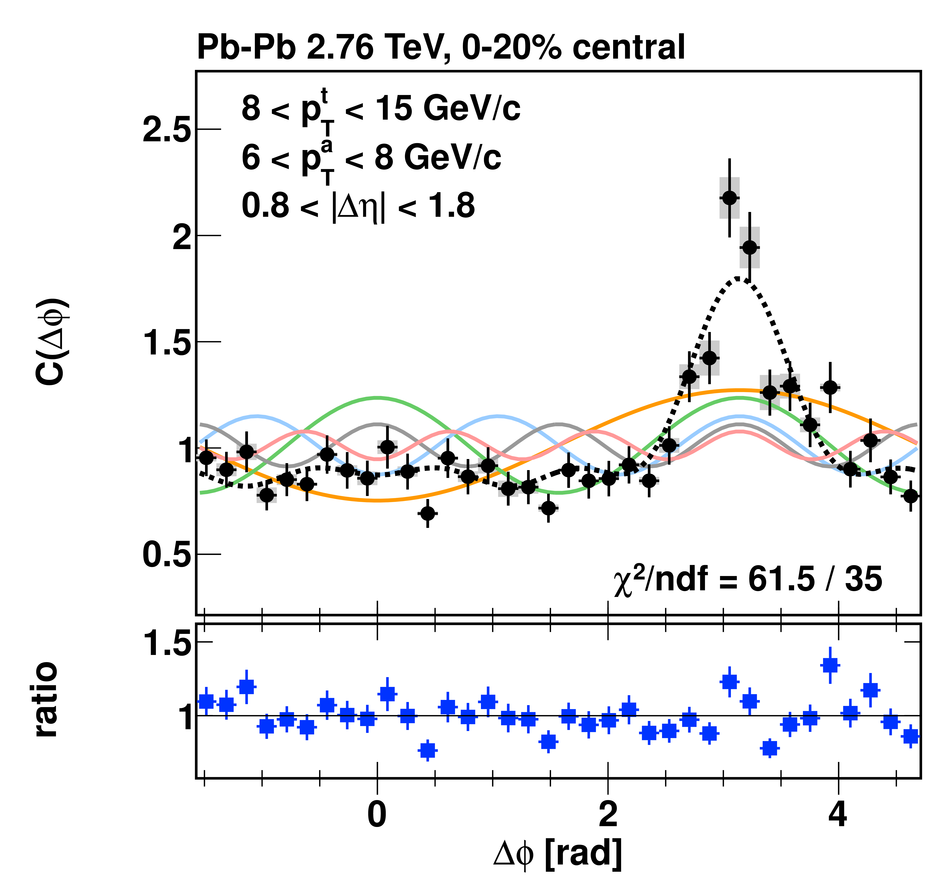
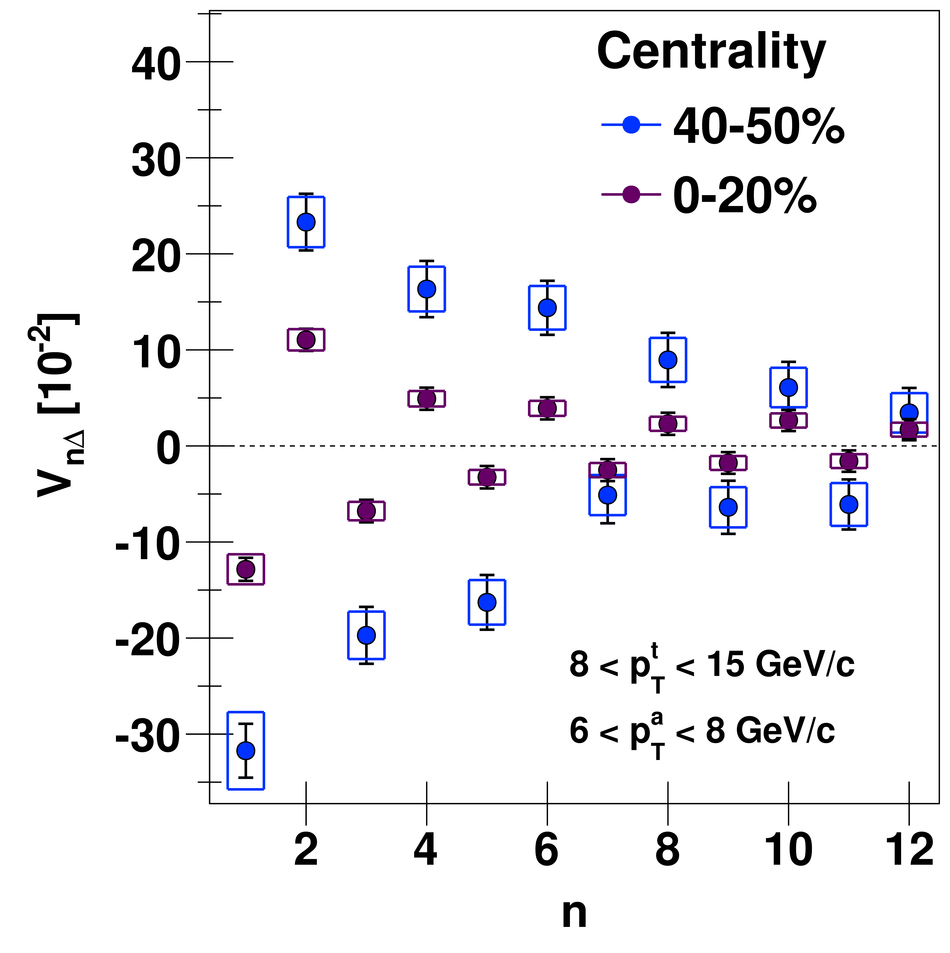
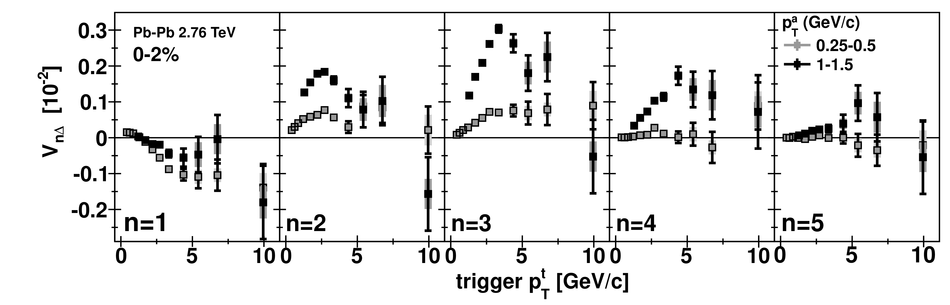
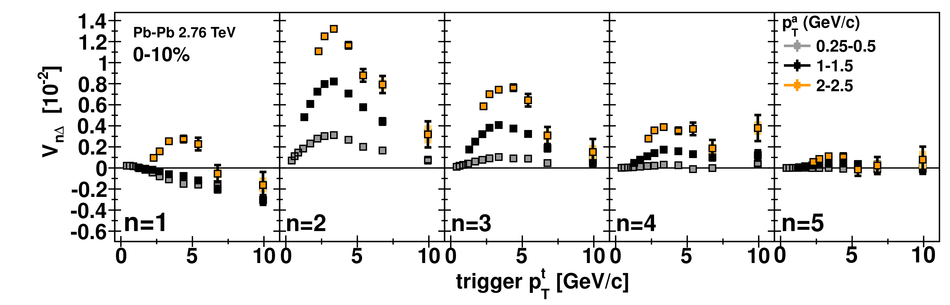
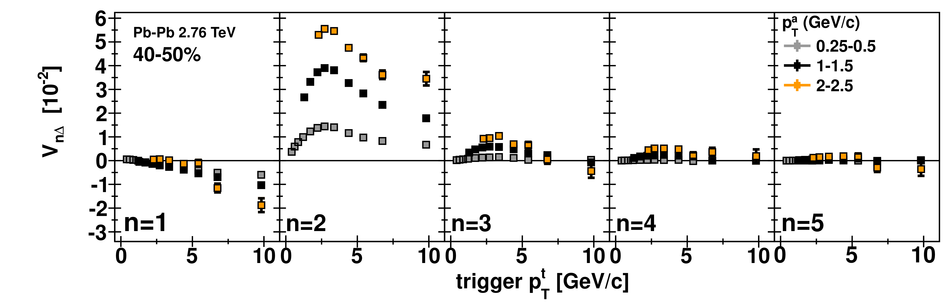
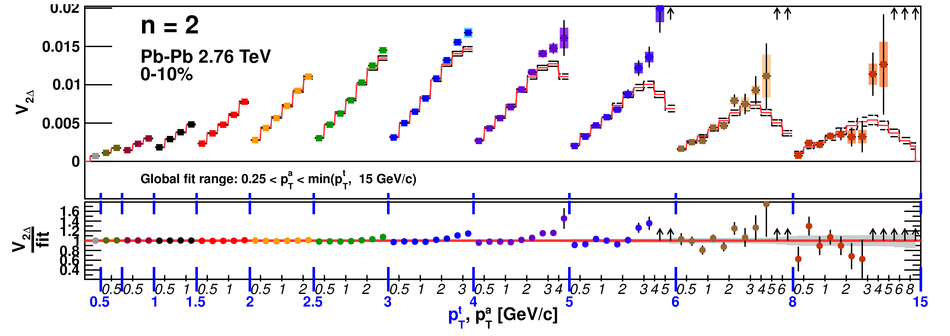
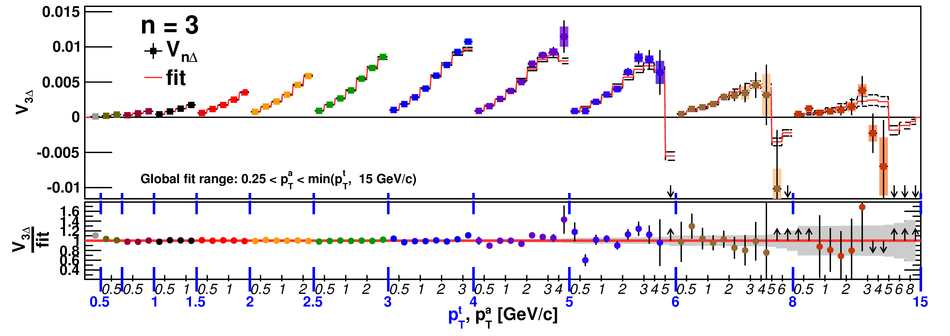
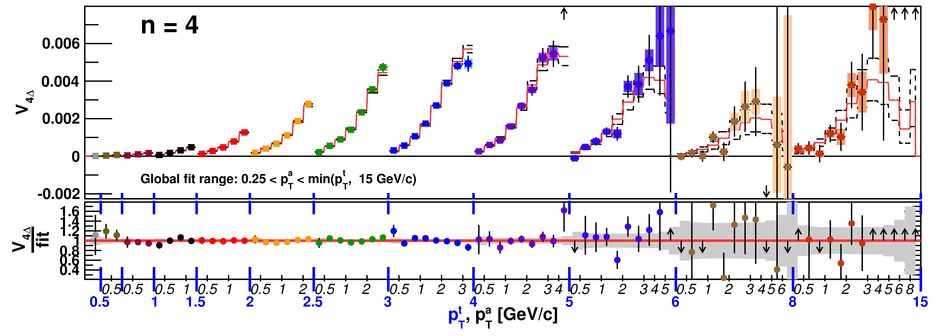
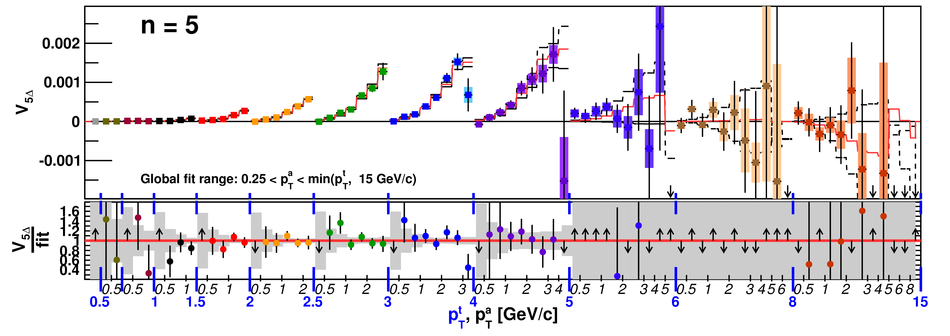
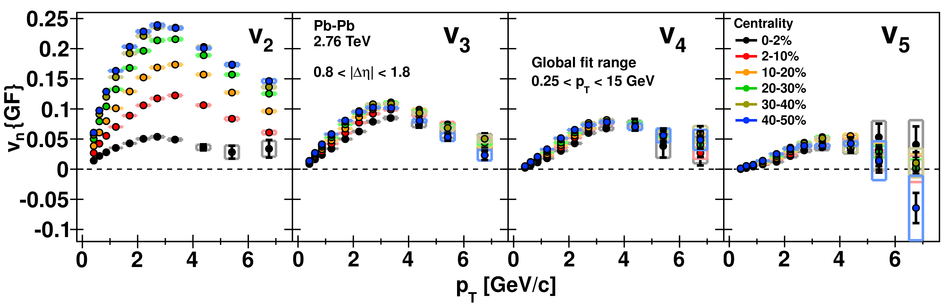
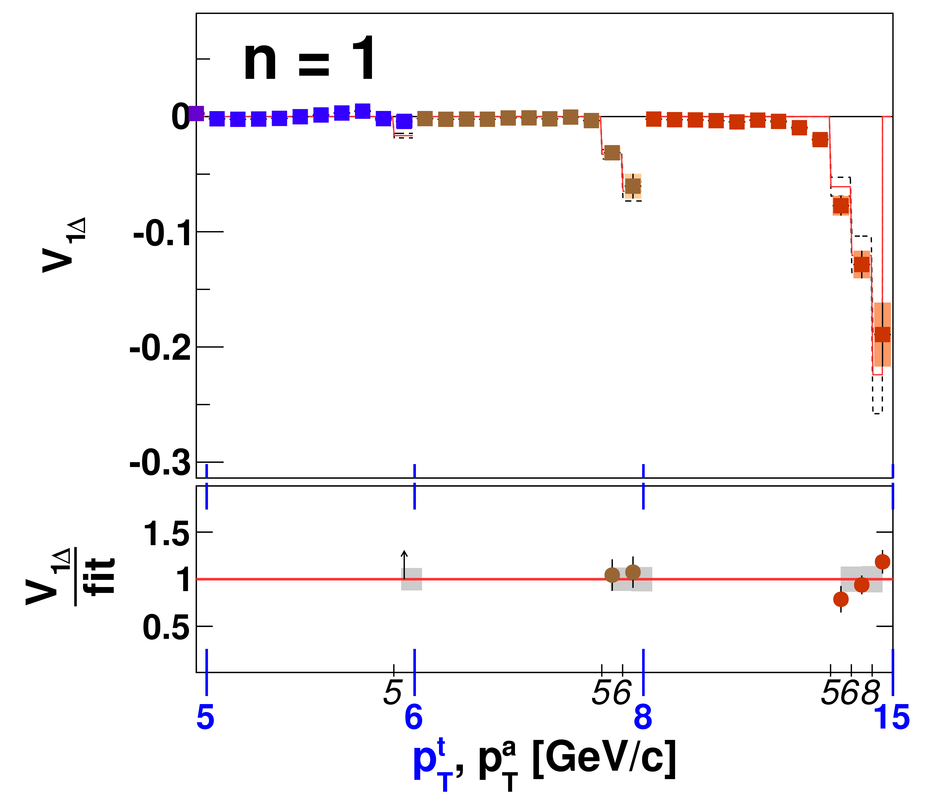
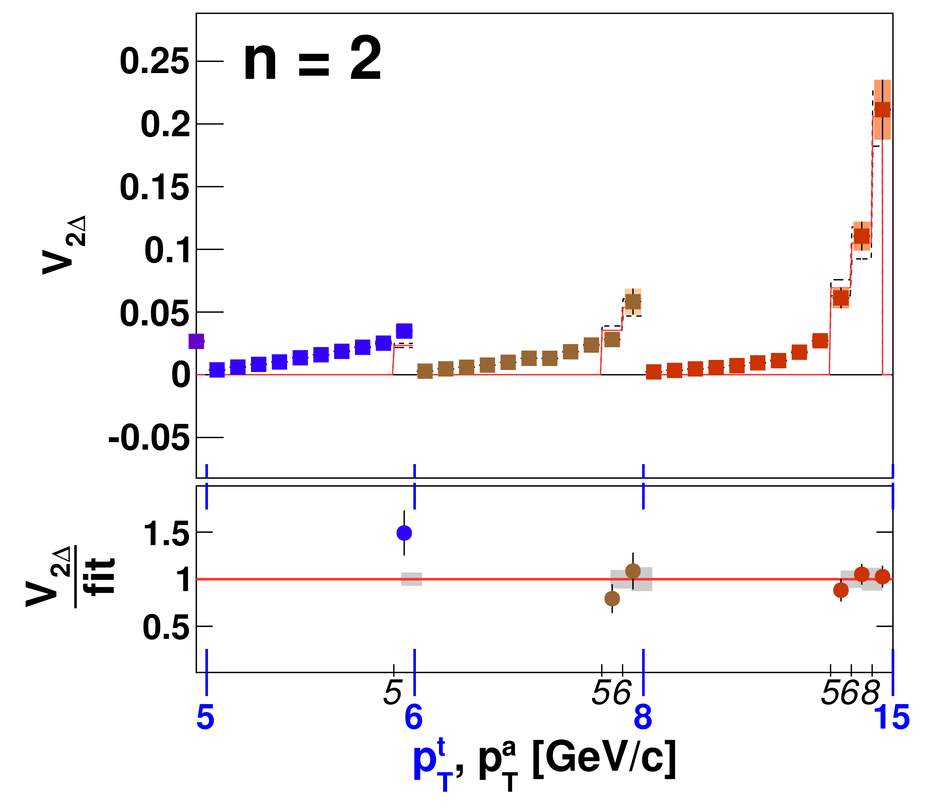
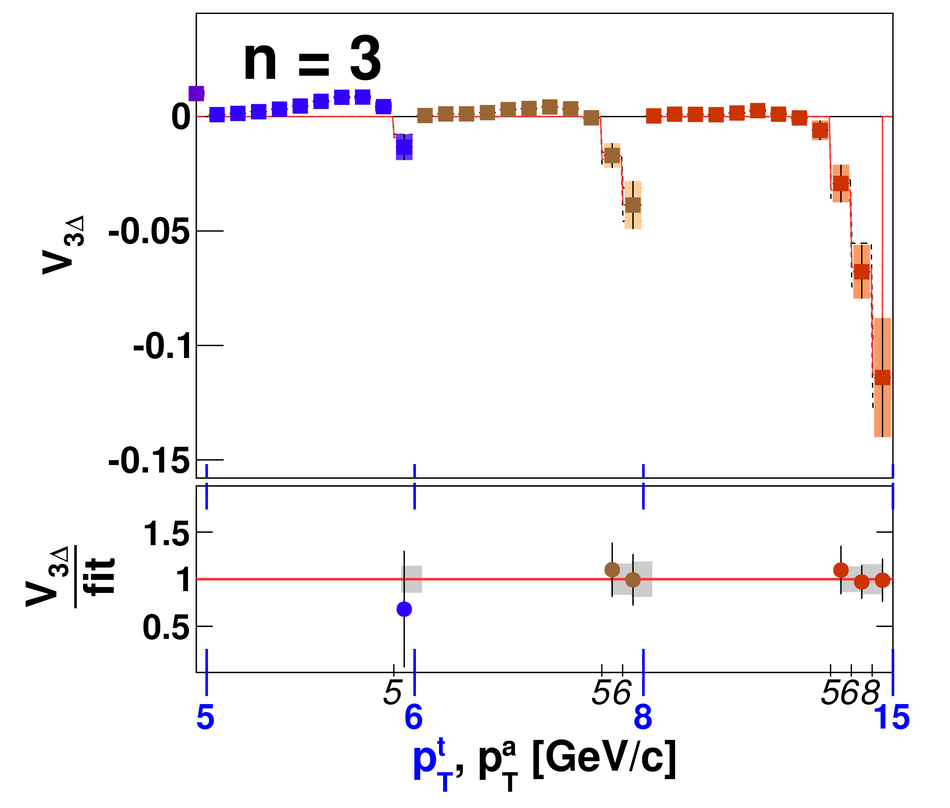
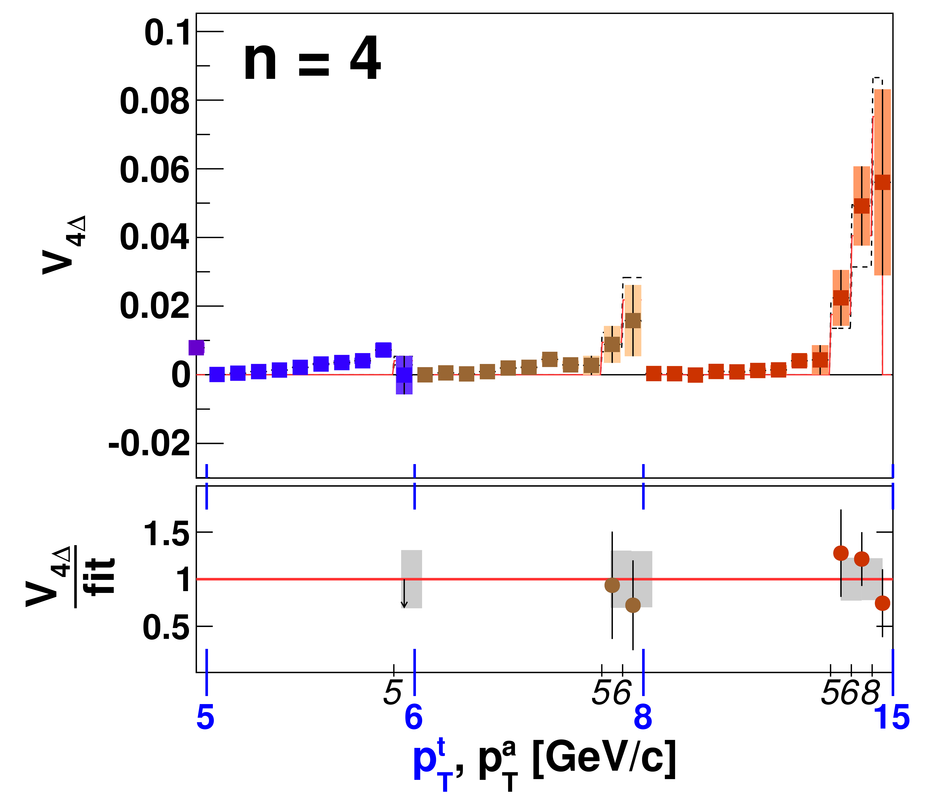
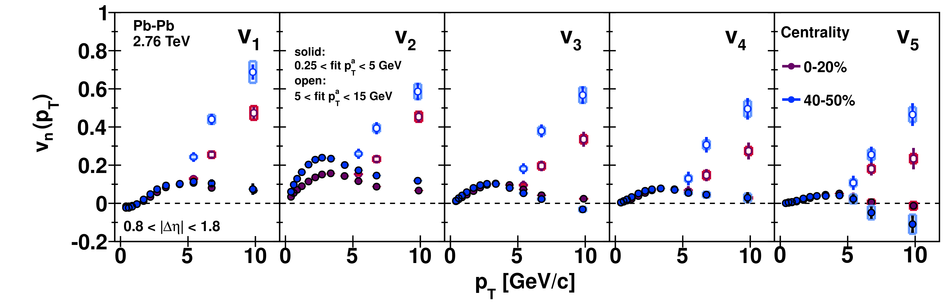
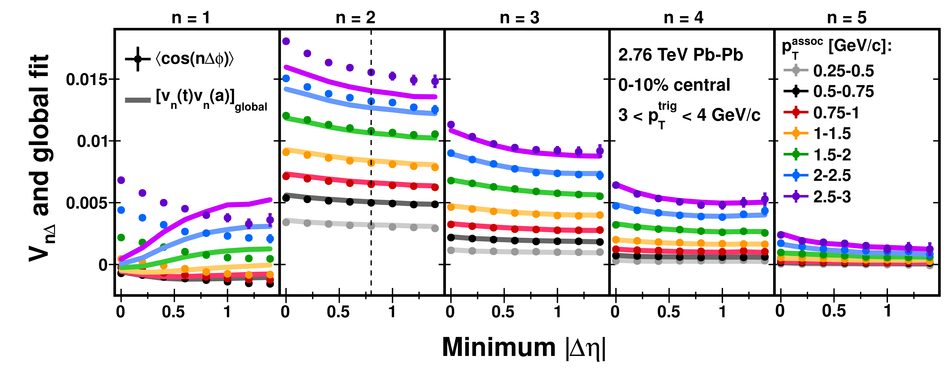
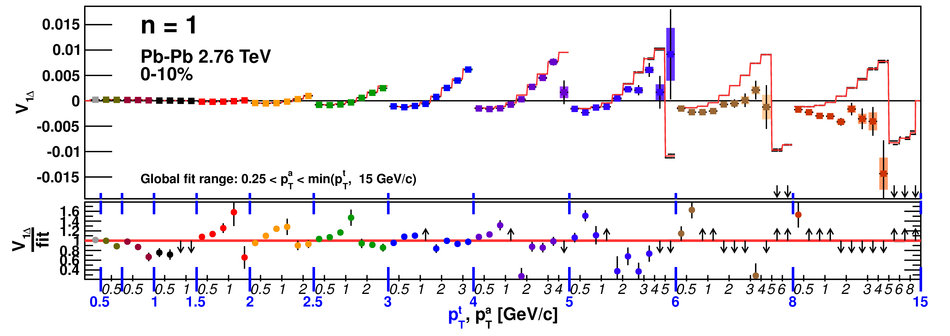
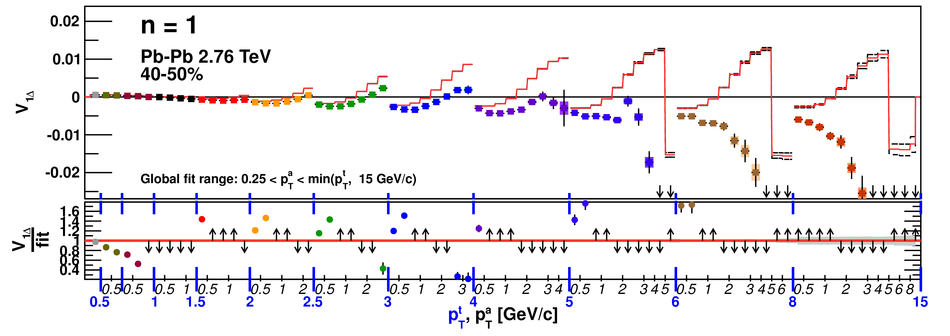
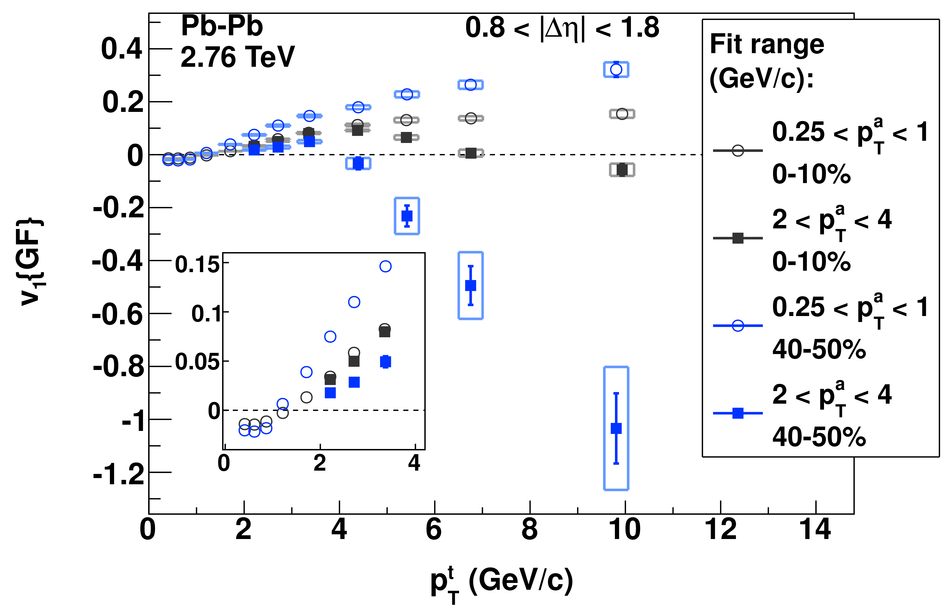
Angular correlations between unidentified charged trigger ($t$) and associated ($a$) particles are measured by the ALICE experiment in Pb-Pb collisions at $\sqrt{s_{\rm NN}}=2.76$ TeV for transverse momenta $0.25 <~ p_{T}^{t,\, a} <~ 15$ GeV/$c$, where $p_{T}^t > p_{T}^a$. The shapes of the pair correlation distributions are studied in a variety of collision centrality classes between 0 and 50% of the total hadronic cross section for particles in the pseudorapidity interval $|\eta| <~ 1.0$. Distributions in relative azimuth $\Delta\phi \equiv \phi^t - \phi^a$ are analyzed for $|\Delta\eta| \equiv |\eta^t - \eta^a| > 0.8$, and are referred to as "long-range correlations". Fourier components $V_{n\Delta} \equiv \langle \cos(n\Delta\phi)\rangle$ are extracted from the long-range azimuthal correlation functions. If particle pairs are correlated to one another through their individual correlation to a common symmetry plane, then the pair anisotropy $V_{n\Delta}(p_{T}^t, p_{T}^a)$ is fully described in terms of single-particle anisotropies $v_n (p_{T})$ as $V_{n\Delta}(p_{T}^t, p_{T}^a) = v_n(p_{T}^t) \, v_n(p_{T}^a)$. This expectation is tested for $1 \leq n \leq 5$ by applying a global fit of all $V_{n\Delta} (p_{T}^t, p_{T}^a)$ to obtain the best values $v_{n}\{GF\} (p_{T})$. It is found that for $2 \leq n \leq 5$, the fit agrees well with data up to $p_T^a \sim 3$-4 GeV/$c$, with a trend of increasing deviation as $p_{T}^t$ and $p_{T}^a$ are increased or as collisions become more peripheral. This suggests that no pair correlation harmonic can be described over the full $0.25 <~ p_{T} <~ 15$ GeV/$c$ range using a single $v_n(p_T)$ curve; such a description is however approximately possible for $2 \leq n \leq 5$ when $p_T^a <~ 4$ GeV/$c$. For the $n=1$ harmonic, however, a single $v_1(p_T$ curve is not obtained even within the reduced range $p_T^a <~ 4$ GeV/$c$.
Phys.Lett. B 708 (2012) 249-264
HEP Data
e-Print: arXiv:1109.2501 | PDF | inSPIRE
CERN-PH-EP-2011-152